Bone Marrow Transplant Data
Bone_Marrow_Transplant_Data.RmdIntroduction
We apply the package stackBagg to a data set The Bone Marrow Transplant Data (bmt) which is in the package timereg . Bone marrow transplants are a standard treatment for acute leukemia. In the recovery process patients can suffer from Infections, toxicity, and (after allogeneic HSCT only), graft-vs.-host disease (GVHD) being the main causes of death. We are interested in predicting the time to death related to treatment where the risk of relapse is a competing risk.
Setup
We load the package stackBagg and timereg and we load the data set bmt
library(stackBagg)
#> Loading required package: Matrix
#> Loading required package: gam
#> Loading required package: splines
#> Loading required package: foreach
#> Loaded gam 1.16.1
library(timereg)
#> Loading required package: survival
bmt.data <- data(bmt)summary(bmt)
#> time cause platelet age
#> Min. : 0.030 Min. :0.0000 Min. :0.0000 Min. :-2.3493
#> 1st Qu.: 2.426 1st Qu.:0.0000 1st Qu.:0.0000 1st Qu.:-0.6336
#> Median : 7.862 Median :1.0000 Median :0.0000 Median : 0.2026
#> Mean : 22.237 Mean :0.8211 Mean :0.3137 Mean : 0.0000
#> 3rd Qu.: 35.806 3rd Qu.:1.0000 3rd Qu.:1.0000 3rd Qu.: 0.7875
#> Max. :110.625 Max. :2.0000 Max. :1.0000 Max. : 1.9396
#> tcell
#> Min. :0.0000
#> 1st Qu.:0.0000
#> Median :0.0000
#> Mean :0.1324
#> 3rd Qu.:0.0000
#> Max. :1.0000
dim(bmt)
#> [1] 408 5
train.set <- sample(1:nrow(bmt), floor(.9*nrow(bmt)), replace=FALSE)
test.set <- setdiff(1:nrow(bmt), train.set)
bmt.train <- data.frame(bmt[train.set,])
bmt.test <- data.frame(bmt[test.set,])
tao=7Let’s define the library of algorithms:
We set the covariates that we include in the models:
Now, we are ready to predict the outcome of interest using all the algorithms:
pred.bmt=stackBagg::stackBagg(train.data = bmt.train,test.data = bmt.test,xnam=xnam,tao=7,weighting ="CoxPH" ,folds =5,ens.library = ens.library )
#>
|
| | 0%
|
|:):):):):):) | 20%
|
|:):):):):):):):):):):):):) | 40%
|
|:):):):):):):):):):):):):):):):):):):) | 60%
|
|:):):):):):):):):):):):):):):):):):):):):):):):):):) | 80%
|
|:):):):):):):):):):):):):):):):):):):):):):):):):):):):):):):):)| 100%The assessment of predictive performance using the IPCW AUC is:
pred.bmt$auc_ipcwBagg
#> ens.glm ens.gam.3 ens.gam.4 ens.lasso ens.randomForest ens.svm
#> [1,] 0.7087876 0.7357849 0.7356652 0.7055677 0.6828238 0.6848676
#> ens.bartMachine ens.knn ens.nn Stack
#> [1,] 0.7191245 0.7190862 0.6848676 0.6855865Now let s take a look at prediction of the algorithms that allows for weights natively:
head(pred.bmt$prediction_native_weights,5)
#> ens.glm ens.gam.3 ens.gam.4 ens.lasso ens.randomForest
#> 1 0.4296483 0.3687665 0.3688015 0.3688015 0.3688015
#> 2 0.6957361 0.2535669 0.2535311 0.2535311 0.2535310
#> 3 0.3996902 0.4798038 0.4799128 0.4799128 0.4799128
#> 4 0.2073166 0.1861105 0.1860391 0.1860391 0.1860390
#> 5 0.1795551 0.2395089 0.2393711 0.2393711 0.2393710and their performance is:
pred.bmt$auc_native_weights
#> ens.glm ens.gam.3 ens.gam.4 ens.lasso ens.randomForest
#> [1,] 0.6986351 0.6799321 0.6799321 0.6799321 0.6799321The prediction of the survival based methods
head(pred.bmt$prediction_survival,5)
#> CoxPH CoxBoost Random Forest
#> [1,] 0.3708020 0.3605007 0.4736565
#> [2,] 0.2736267 0.2784543 0.5008048
#> [3,] 0.4707669 0.4416556 0.4046919
#> [4,] 0.2093228 0.2205586 0.2456751
#> [5,] 0.2282168 0.2396609 0.2649929Lastly, we could see the performance of the algorithms if we were to discard the censored observations
pred.discard <- stackBagg::prediction_discard(train.data = bmt.train,test.data = bmt.test,xnam=names(bmt)[-(1:2)],tao=7,ens.library=ens.library)
head(pred.discard$prediction_discard)
#> ens.glm ens.gam.3 ens.gam.4 ens.lasso ens.randomForest ens.svm
#> 1 0.3952584 0.44 0.4016965 0.3373199 0.4297783 0.3778363
#> 2 0.2720310 0.32 0.4562393 0.3284920 0.6977343 0.2613326
#> 3 0.4730285 0.40 0.4446211 0.3448453 0.4137467 0.4890965
#> 4 0.1993480 0.20 0.2459319 0.3357070 0.2137196 0.1940605
#> 5 0.2678665 0.36 0.2287836 0.3112569 0.1629799 0.2464748
#> 6 0.1714913 0.28 0.1997799 0.3335530 0.1499076 0.1743182
#> ens.bartMachine ens.knn ens.nn
#> 1 0.4177470 0.4181522 0.3778628
#> 2 0.2845658 0.3009119 0.2613058
#> 3 0.4696340 0.4621833 0.4891776
#> 4 0.2290154 0.2293746 0.1940062
#> 5 0.2762601 0.2754645 0.2463706
#> 6 0.2088973 0.2105355 0.1742594
pred.discard$auc_discard
#> ens.glm ens.gam.3 ens.gam.4 ens.lasso
#> 0.6828645 0.7276215 0.7480818 0.6572890
#> ens.randomForest ens.svm ens.bartMachine ens.knn
#> 0.6994885 0.6777494 0.7109974 0.7161125
#> ens.nn
#> 0.6777494The ROC curve of the stack is
stackBagg::plot_roc(time=bmt.test$time,delta = bmt.test$cause,marker =pred.bmt$prediction_ensBagg[,"Stack"],wts=pred.bmt$wts_test,tao=7,method = "ipcw")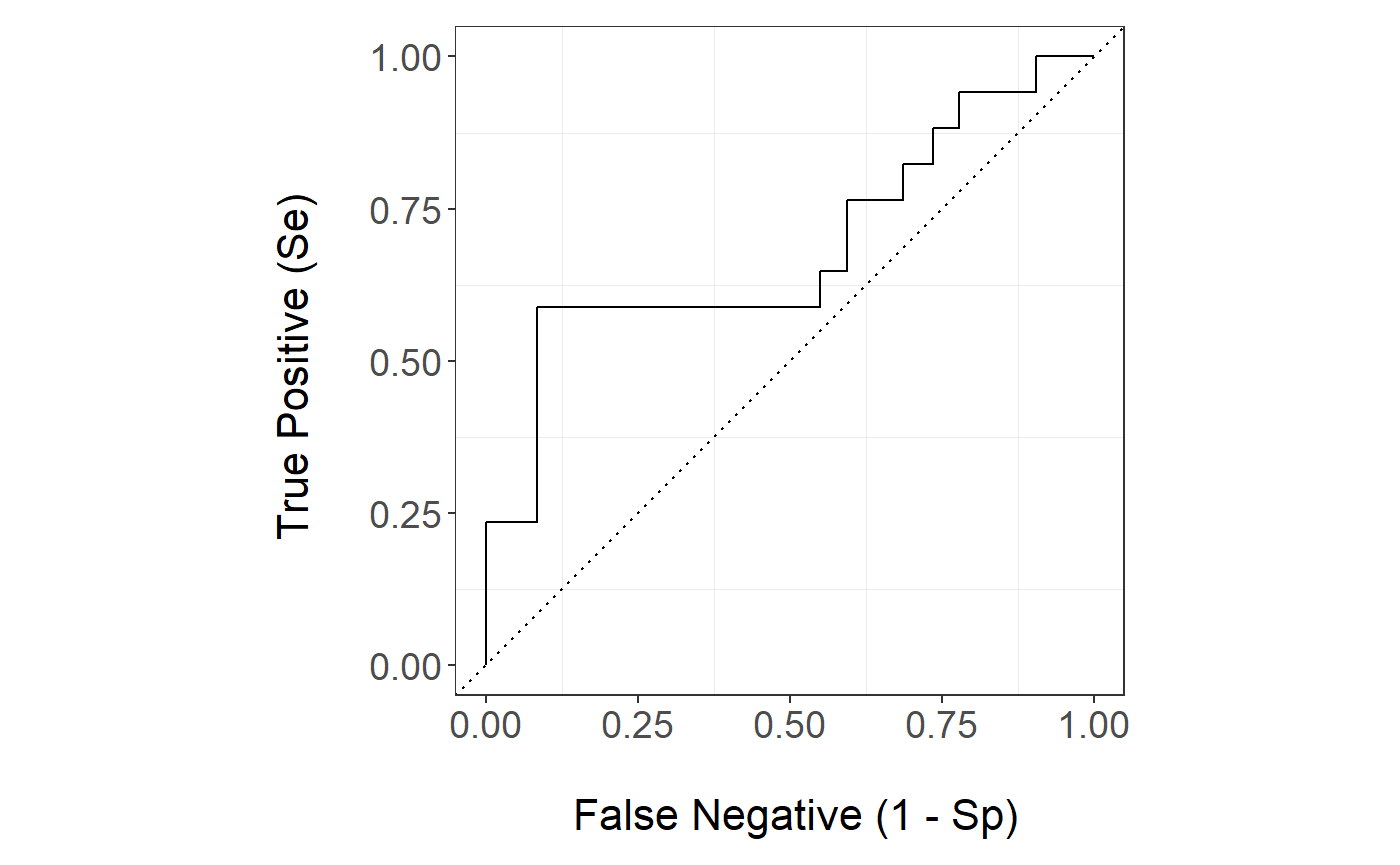
The Random Forest ROC curve is
stackBagg::plot_roc(time=bmt.test$time,delta = bmt.test$cause,marker =pred.bmt$prediction_ensBagg[,"ens.randomForest"],wts=pred.bmt$wts_test,tao=7,method = "ipcw")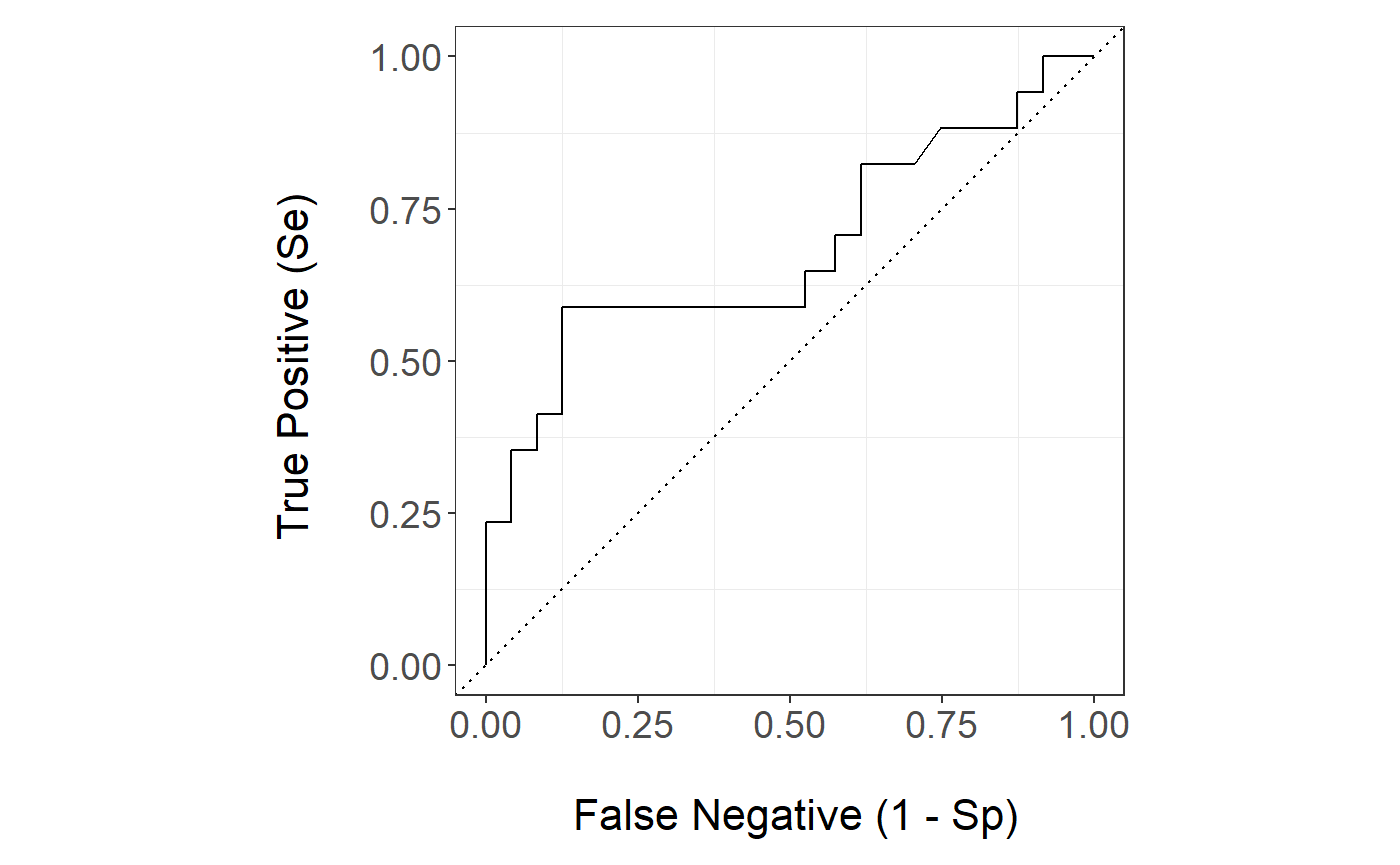
The Random Forest survival ROC curve is
stackBagg::plot_roc(time=bmt.test$time,delta = bmt.test$cause,marker =pred.bmt$prediction_survival[,"Random Forest"],wts=pred.bmt$wts_test,tao=7,method = "ipcw")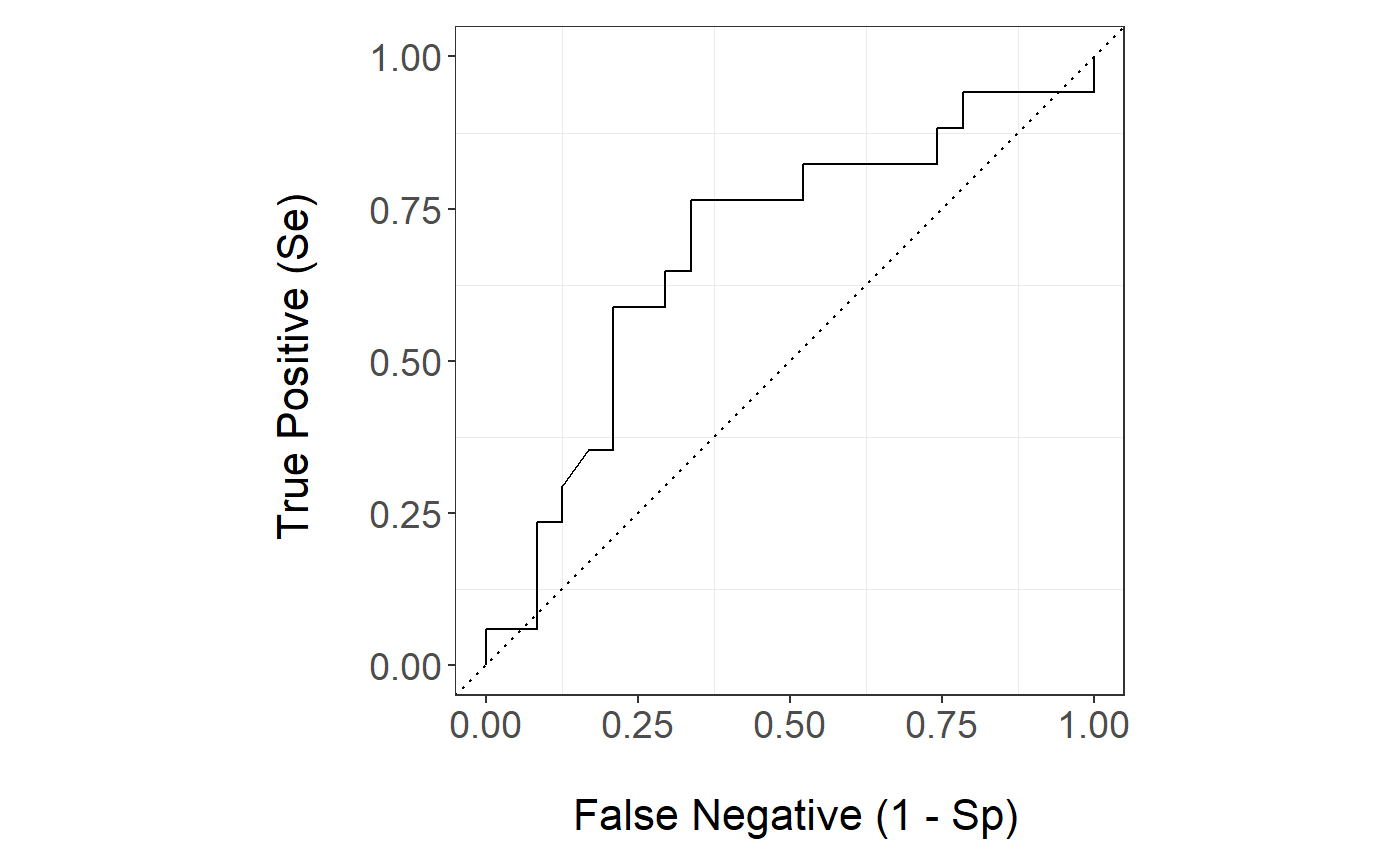
The Random Forest natively weighted ROC curve is
stackBagg::plot_roc(time=bmt.test$time,delta = bmt.test$cause,marker =pred.bmt$prediction_native_weights[,"ens.randomForest"],wts=pred.bmt$wts_test,tao=7,method = "ipcw")
The Random Forest discarding censored observations
stackBagg::plot_roc(time=bmt.test$time,delta = bmt.test$cause,marker =pred.discard$prediction_discard[,"ens.randomForest"],tao=7,method = "discard")
#> NULL